
Il Machine Learning è un campo di studi meraviglioso.
Durante la mia esperienza come insegnante di Machine Learning e Data Science a DataMasters è capitato più di una volta che degli studenti andassero in confusione su concetti legati al mondo della statistica che è bene tenere in mente da subito, e che troppo spesso si danno per scontati. Mi riferisco soprattutto a indici come la varianza, la deviazione standard, la covarianza, etc.: meno intuitivi rispetto ad indici più semplici (come media o mediana) o comunque meno conosciuti da coloro che si approcciano per la prima volta allo studio del machine learning senza avere un background statistico di base.
In questo articolo presenterò proprio questi indici, esaminandoli brevemente dal punto di vista teorico per poi calcolarli in maniera manuale con dei semplici esempi e fare delle considerazioni sul significato dei valori che otterremo. In particolare, parleremo di 3 indici:
- varianza
- deviazione standard
- covarianza
Partiamo dalla teoria. C’è da dire innanzitutto che questi indici sono legati in qualche modo alla media. Ergo, prima di calcolare questi indici dobbiamo assolutamente calcolare la media aritmetica di un insieme di dati:
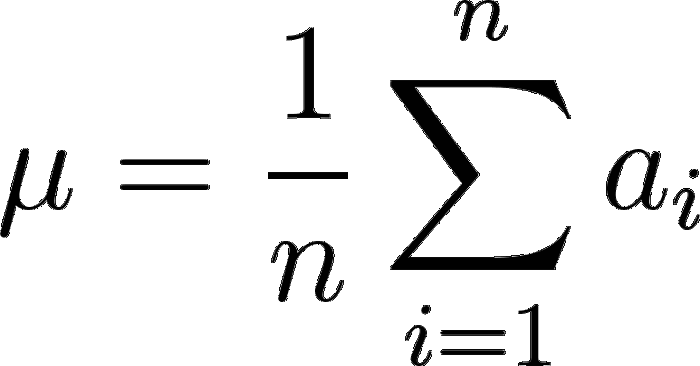
Media aritmetica. Facile, no?
Semplicissimo: si prendono tutti i dati a nostra disposizione, si sommano e si dividono per il loro numero.
Varianza e deviazione standard sono degli indici che definiscono la variabilità di un insieme di dati (di una distribuzione) rispetto alla loro media aritmetica. La variabilità descrive quanto i punti del nostro dataset siano lontani fra loro e dal centro di una distribuzione (nel nostro caso, dal valore medio). Quindi variabilità più alta significa avere punti più “sparsi”, mentre variabilità più bassa significa avere punti più compatti.
La differenza più importante fra varianza e deviazione (che sono molto legate fra loro, come vedremo) risiede nell’unità di misura utilizzata:
- la varianza è espressa nell’unità di misura del dataset originario al quadrato, motivo per cui non è di visualizzazione immediata
- la deviazione standard è espressa nella stessa unità di misura del dataset originario, ed è quindi un po’più semplice da visualizzare anche mentalmente
La formula per calcolare la varianza su tutto un insieme di dati (d’ora in poi detto volgarmente dataset) è:
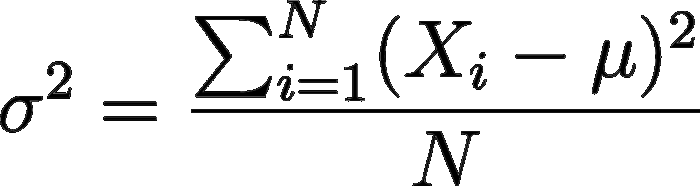
Calcolo della varianza. Non abbiate paura di Σ!
Semplicemente, per ogni elemento del nostro dataset:
- sottraiamo la media aritmetica
- eleviamo al quadrato la differenza calcolata
Dopo aver fatto queste operazioni sommiamo tutti i quadrati delle differenze così calcolati e dividiamo questa quantità per il numero totale di elementi del dataset.
Se al posto di calcolare la varianza su tutto il dataset la calcoliamo solo su un campione del dataset di partenza dobbiamo ricordare di:
- usare la media del campione, e non la media del dataset
- dividere per N — 1 (dove N è la dimensione del campione e non quella del dataset)
Di contro, la deviazione standard si ottiene semplicemente calcolando la radice quadrata della varianza:
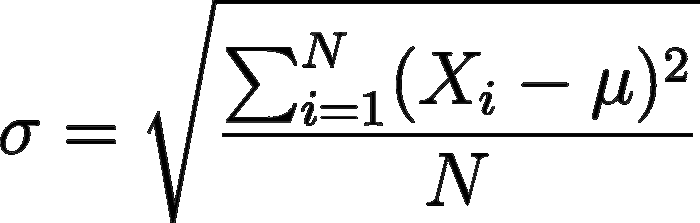
Miss Deviazione Standard, vale a dire la radice quadrata della varianza
Valgono ovviamente le regole già viste per la varianza se usiamo la popolazione totale o un campione del dataset.
Prendiamo ora dei dati di esempio e calcoliamo sia la varianza che la deviazione standard. Diciamo che abbiamo questi numeri:
46
69
32
60
52
41
Qual è il significato di questi numeri? In questo caso nessuno in particolare, sono i nostri dati di partenza. Potrebbero essere le quantità di mele presenti in 6 diversi negozi di ortofrutta, o il diametro delle circonferenze craniche di 6 esemplari di un qualche strano animale. Diciamo che in questo caso rappresentano i pesi espressi in kg di 6 persone diverse.
Calcoliamo la media aritmetica:
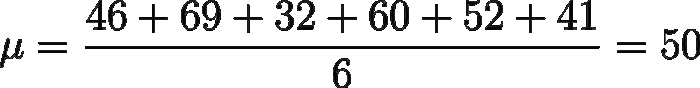
Calcoliamo adesso il quadrato della differenza dalla media di ogni elemento del dataset:
(46–50)² = (-4)² = 16kg²
(69–50)² = (19)² = 361kg²
(32–50)² = (-18)² = 324kg²
(60–50)² = (10)² = 100kg²
(52–50)² = (2)² = 4kg²
(41–50)² = (-9)² = 81kg²
Adesso sommiamo tutti questi valori e dividiamoli per N:

Tutto qui. That’s it. Mettiamo questo risultato sotto radice per calcolare anche la deviazione standard:
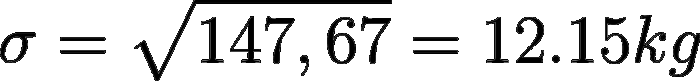
L’analisi della deviazione standard è più intuitiva di quella della varianza proprio perché l’unità di misura è la stessa dei dati di partenza. In questo caso (occhio allo scioglilingua) possiamo dire che ogni campione, in media, devia dalla media di 12.15kg. Parlando di deviazione standard, è bene ricordare la regola empirica del 68–95–99.7. Essa dice che in una distribuzione gaussiana (o normale) di dati:
- il 68% dei campioni ricade nell’intervallo [µ — σ, µ + σ]
- il 95% dei campioni ricade nell’intervallo [µ — 2σ, µ + 2σ]
- il 99.7% dei campioni ricade nell’intervallo [µ — 3σ, µ + 3σ]
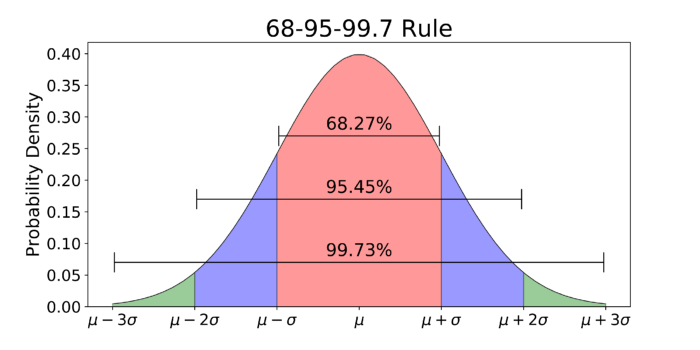
Regola del 68–95–99.7 in una distribuzione gaussiana a media µ
Manteniamoci ancora su semplici serie numeriche e cerchiamo di capire cosa è la covarianza.
Innanzitutto quando parliamo di covarianza non ci limitiamo più ad osservare una singola variabile (nel nostro caso il peso di alcune persone espresso in kg), ma introduciamo un’altra variabile. La covarianza è un indice che mette in relazione due variabili; in particolare, a differenza di altri indici (uno su tutti: la correlazione), la covarianza definisce la relazione direzionale fra due variabili. I valori ammessi della covarianza sono compresi fra -infinito e +infinito. Per “relazione direzionale” intendiamo dire che:
- se la covarianza ha un valore positivo, le due variabili oggetto del nostro studio si muovono in maniera concorde;
- se la covarianza ha un valore negativo, le due variabili oggetto del nostro studio si muovono in maniera discorde;
- se la covarianza è pari a zero, le due variabili non sono correlate fra loro
La formula per il calcolo della covarianza è la seguente:
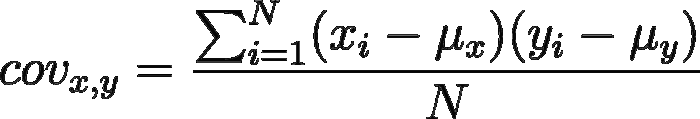
Covarianza, vale a dire: come sono legate fra loro due variabili casuali?
Come in precedenza, se calcoliamo la covarianza fra due campioni del dataset di partenza bisogna sottrarre i valori dei singoli campioni alla media del campione e dividere per il numero di elementi nel campione — 1.
Supponiamo di avere un altro insieme di dati e mettiamolo in relazione al primo già esaminato calcolando la covarianza fra le due serie:
150
176
142
165
154
147
Diciamo che questi valori rappresentano le altezze in centimetri delle stesse persone per cui abbiamo misurato i pesi in precedenza. Calcoliamo anche qui la media aritmetica: 155.66 (basta sommare fra loro questi numeri e dividerli per 6).
Calcoliamo adesso le differenze nel caso della variabile X e della variabile Y, e moltiplichiamole fra loro.
(46–50) * (150–155) = -4 * -5 = 20
(69–50) * (176–155) = 19 * 21 = 399
(32–50) * (142–155) = -18 * -13 = 234
(60–50) * (165–155) = -10 * 10 = -100
(52–50) * (154–155) = -2 * -1 = 2
(41–50) * (147–155) = -9 * -8 = 72
Adesso sommiamo questi valori e dividiamoli per 6:
(20 + 399 + 234 -100 + 2 + 72)/6 = 104.5
Notiamo che l’unità di misura è kg-cm. L’unità di misura della covarianza, in genere, è un’unità di misura che dipende esclusivamente dalle unità di misura delle due variabili di cui vogliamo calcolare la covarianza. Il valore ottenuto è positivo, e questo dice che esiste un certo grado di relazione fra le due variabili: evidentemente quando ci sono dei valori di peso più alti, ci sono dei valori più alti anche per l’altezza. Se invece ci fosse stata una tendenza dei valori alti di X a co-esistere con valori più bassi di Y la covarianza sarebbe stata negativa.
In caso abbiamo più variabili e vogliamo calcolare la covarianza fra di esse si parla di matrice di covarianza. Non la calcoleremo a mano (avete presente la storia secondo cui i programmatori sono pigri? Ecco.), ma dal punto di vista concettuale è molto semplice. Si tratta di una matrice quadrata in cui le intestazioni delle righe sono le nostre variabili e le colonne anche. Se ad esempio volessimo calcolare la matrice di covarianza delle variabili appena viste, avremmo questo:
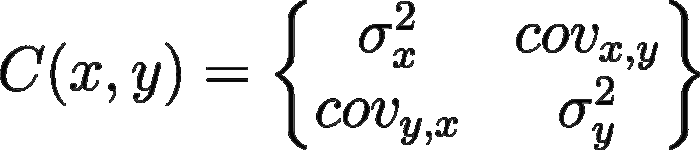
Matrice delle covarianze
È una matrice simmetrica (perchè cov(x, y) = cov(y, x)) e notiamo che sulla diagonale principale troviamo le varianze delle singole variabili X e Y. Gli altri elementi sono le covarianze delle variabili corrispondenti. Un esempio a 3 variabili disegnato con la libreria Python seaborn:
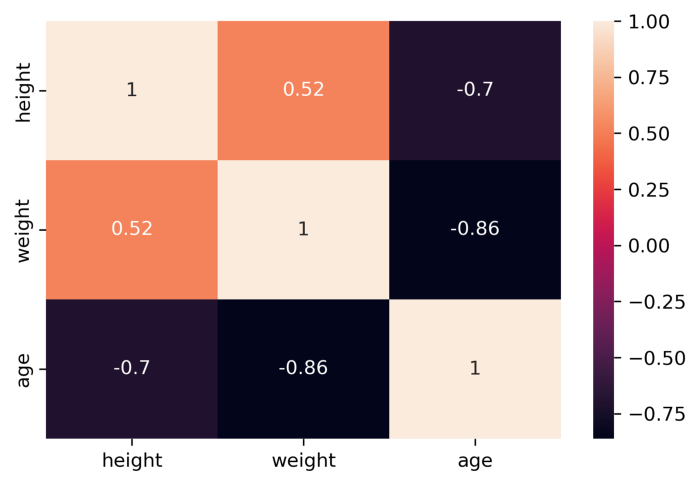
Un esempio a 3 variabili
I significati non cambiano. Ad esempio prendiamo la riga “height” e la colonna “age”. La casella alla prima riga e all’ultima colonna rappresenta la covarianza fra le due variabili (-0.7), e il fatto che è negativa ci dice che le due variabili hanno un comportamento piuttosto discorde. Di contro, la covarianza fra height e weight è pari a 0.52, e quindi potremmo dire che fra queste due variabili c’è una certa concordanza.
Insomma, come avete potuto notare, dietro nomi altisonanti spesso si celano concetti semplici che possono essere padroneggiati senza troppi patemi d’animo, e dietro formule astruse spesso si nascondono calcoli più facili a farsi che a dirsi. Morale della favola: non abbiate paura di varianza, deviazione standard e covarianza! È tutto molto più facile di quanto sembra!
Giuseppe Mastrandrea – Machine Learning Specialist












