
Negli scorsi articoli di questa mini-serie (perlopiù basata sulle difficoltà che gli studenti di DataMasters hanno dimostrato di avere) sugli indici statistici abbiamo già visto cosa sono varianza, deviazione standard, covarianza e correlazione. Con questo articolo approfondiamo una struttura dati introdotta nello scorso articolo e che quando ho iniziato a studiare Machine Learning mi ha letteralmente fatto esplodere il cervello, e non perchè fosse un concetto difficile, ma perchè mi ha realmente aperto la porta delle potenzialità della Data Science e del Machine Learning.
Dove eravamo rimasti? La correlazione
La struttura dati di cui sto parlando è la matrice di correlazione. È anch’esso, come molti altri, un concetto molto semplice da capire e ancora più semplice da utilizzare. Ovviamente si parte dal concetto di correlazione: la correlazione è una misura che indica la relazione lineare fra due variabili casuali. È compresa sempre fra -1 e 1, dove:
- -1 significa che le due variabili hanno una relazione lineare inversa, vale a dire che all’aumentare di una, l’altra diminuisce
- 1 significa che le due variabili hanno una relazione lineare diretta, vale a dire che all’aumentare di una aumenta anche l’altra
- 0 significa che non è possibile stabilire fra le due variabili un andamento lineare
Occhio, correlazione non significa causalità. Ad esempio, quando la correlazione fra due variabili è vicina ad 1, non significa che un cambio in una variabile generi automaticamente un cambio anche nella seconda. Ad esempio, prendiamo due variabili come “Numero di gelati venduti giornalmente nell’arco di un anno” e “Numero di scottature giornaliere rilevate nell’arco di un anno”. Verosimilmente le due variabili avranno un’alta correlazione (all’aumentare di una aumenterà verosimilmente anche l’altra), ma un cambio in una delle due variabili sicuramente non si rifletterà nell’altra. Alta correlazione, bassa causalità.
Fissato questo concetto, torniamo alla matrice di correlazione.
Matrice di correlazione
La matrice di correlazione è una matrice quadrata (il che significa che il numero di righe è uguale al numero di colonne) simmetrica (il che significa che la matrice di correlazione è uguale alla sua trasposta) con gli elementi della diagonale principale tutti uguali ad 1 e semidefinita positiva (significa che i suoi autovalori sono tutti non negativi). Mentre le prime due proprietà sono di semplice intuizione e visualizzazione, è bene spendere un paio di parole sull’ultima proprietà, perchè non tutte le matrici quadrate, simmetriche con diagonale principale pari a 1 sono semidefinite positive e quindi non tutte le matrici che soddisfano i primi 3 criteri sono delle matrici di correlazione. Ad esempio, la matrice:

ha un autovalore negativo. Potreste trovarlo a mano, ma visto che abbiamo fretta, usiamo Python e numpy per calcolare tutti i suoi autovalori:

la funzione np.linalg.eig prende in input una matrice (che nei linguaggi di programmazione sono di base delle liste di liste, o vettori di vettori, o array di array) e restituisce una tupla con 2 elementi:
- il primo è costituito dagli autovalori della matrice
- il secondo è costituito dagli autovettori normalizzati della matrice
Ergo per accedere ai singoli autovalori bisogna accedere all’elemento con indice [0] della tupla restituita.
Esistono delle tecniche per rendere semidefinita positiva una matrice inizialmente non semidefinita positiva, ma non approfondiremo queste tecniche in questo articolo. Qui alcuni spunti interessanti per chi vuole approfondire la questione.
Costruire una matrice di correlazione
Cerchiamo adesso di capire come è fatta una matrice di correlazione, supponendo che abbia tutte le proprietà di cui abbiamo già parlato.
Partiamo da un dataset, ovvero da un insieme di variabili casuali, o se preferite da un insieme di righe che costituiscono singole osservazioni e in cui ciascuna riga è divisa in un certo numero di colonne.
Quando ho studiato per la prima volta ML da questo libro, uno dei primi esempi di modelli predittivi (una semplicissima regressione lineare) si riferiva ad un dataset formato dalle quotazioni delle case nei diversi quartieri dello stato della California. Una volta scoperta cos’è la regressione lineare, e soprattutto una volta studiata la parte relativa alle correlazioni e alle matrici di correlazione le mie porte della percezione si sono spalancate, come scriveva qualcuno, però senza mescalina. Sì, a noi informatici basta poco per andare in trip. Comunque: ogni riga del dataset rappresenta un quartiere diverso; ogni riga ha le seguenti feature (N.B. feature è un nome cool per dire “variabile casuale”, o ancora meglio variabile su cui si possono calcolare degli indici statistici):
- longitudine
- latitudine
- età mediana delle case
- numero totale di stanze
- numero totale di stanze da letto
- popolazione
- n. occupanti
- reddito mediano degli occupanti
- valore mediano delle case
- vicinanza all’oceano
Il libro di testo citato è un vero e proprio must per chi vuole studiare Machine Learning, pur avendo dei prerequisiti di base non banali, soprattutto in ambito di programmazione. Tutto il codice del libro è disponibile gratuitamente a questo link, mettetelo fra i preferiti.
Possiamo dire che il dataset in questo caso ha dimensioni n x 10, dove n è il numero di righe presenti nel dataset, cioè il numero di quartieri.
Proviamo a costruire la matrice di correlazione di questo dataset. Le variabili fra cui calcoleremo la correlazione sono le 10 feature del nostro dataset. In realtà c’è una variabile in particolare per cui non ha senso calcolare la correlazione: si tratta della feature “ocean_proximity”, che non è numerica ma categorica. Significa che il suo dominio non è un insieme numerico continuo ma un insieme discreto di valori. In particolare, per questa feature gli unici valori ammessi sono:

Non ha senso calcolare la correlazione (un indice che serve a calcolare la relazione lineare fra due variabili casuali continue) di una variabile con questa feature. Ergo possiamo escluderla anche dalla matrice di correlazione. Iniziamo dalle basi, quindi. Il nostro dataset è inizialmente costituito da 10 feature ma abbiamo deciso di escluderne una, quindi la nostra matrice di correlazione sarà quadrata, di dimensioni 9×9, inizialmente vuota:

Una matrice quadrata vuota.
Iniziamo adesso a riempire la nostra matrice di correlazione con i valori di correlazione. Ricordiamo che ogni elemento di una matrice è indicato da un indice di riga e un indice di colonna. Partiamo da 0 a contare le righe e le colonne, in maniera che (per esempio) l’elemento più in basso a sinistra abbia posizione 8, 0(riga 8, colonna 0). Di contro l’elemento più a destra della quarta riga avrà posizione 3, 8(riga 3, colonna 8). Il fatto che la matrice sia simmetrica impone un vincolo sulla costruzione della tabella, visto che l’elemento con posizione i, j deve avere pari valore dell’elemento in posizione j, i (l’elemento in posizione 3, 8 deve essere uguale all’elemento in posizione 8, 3). Ottenere questa condizione è in realtà molto semplice: partiamo per esempio dalla feature “Longitudine”. Assegniamo la longitudine alla riga con indice 0. La condizione di simmetria rispetto alla diagonale principale (cioè la diagonale che va dall’elemento con indice 0, 0 all’elemento con indice 8, 8)si ottiene assegnando una variabile già assegnata ad una certa riga alla colonna con lo stesso indice: 0. Dopodichè facciamo la stessa cosa con “Latitudine”. Assegniamo la latitudine alla riga con indice 1 e alla colonna con lo stesso indice. Così via fino ad ottenere questa assegnazione di righe e colonne:

Una matrice di correlazione pronta ad essere riempita con le correlazioni.
A questo punto proviamo a leggere la matrice: l’elemento con indice 0, 5 (riga 0, colonna 5) rappresenta la correlazione fra longitudine e popolazione; è per la proprietà di simmetria uguale all’elemento con indice 5, 0, che sarà la correlazione fra popolazione e longitudine. Ricordiamo che la correlazione di due variabili X, Y è uguale alla correlazione di Y, X. Analogamente l’elemento con indice 6, 7 conterrà la correlazione fra “households” e “median_income”, e sarà uguale all’elemento simmetrico con indice 7, 6, che conterrà la correlazione fra “median_income” e “households”. Prendiamo adesso un elemento della diagonale principale, per esempio quello con posizione 4, 4: esso indicherebbe la correlazione fra la feature “total_bedrooms” e se stessa. Per definizione la correlazione di una variabile con se stessa è sempre 1, e discorso analogo vale per tutti gli altri elementi della diagonale principale, che rappresentano la correlazione delle rispettive variabili casuali con se stesse. Quindi tutti gli elementi della diagonale principale di una matrice di correlazione sono uguali a 1.
Matrice di correlazione in Python, pandas e seaborn
Ora: per riempire la matrice di correlazione dovremmo calcolarle per ogni coppia di variabili. Un po’noioso, no? Il calcolo è lasciato come utile esercizio per il lettore. Oppure potremmo usare la libreria Python pandas:

Dopo le istruzioni di import del package `pandas`, leggiamo il file con il metodo di pandas read_csv, che prende come unico argomento di input il path del file, e memorizziamo il risultato della lettura nella variabile housing. Il tipo di dato restituito da housing è un DataFrame, un tipo proprietario di pandas che rappresenta un dataset. Su un dataset è possibile utilizzare una serie di metodi fra cui il metodo corr(), che come dice il nome stesso produce una matrice di correlazione. Per rendere più leggibile la struttura dati con seaborn effettuiamo anche l’arrotondamento a 2 cifre decimali delle correlazioni tramite il metodo round(), al quale passiamo come argomento esattamente il numero di cifre decimali che vogliamo preservare. Nell’istruzione successiva andiamo a stampare l’insieme delle correlazioni per la feature median_income, visualizzata sotto forma di Series di pandas. Si tratta di una struttura dati molto simile ad un array (tant’è che è possibile accedere ai suoi elementi utilizzando l’indice numerico). Possiamo accedere ad un particolare valore anche specificando un secondo indice contenente il nome della variabile di cui vogliamo sapere la correlazione con median_income. Ad esempio:
contiene il valore di correlazione fra le feature median_income e housing_median_age. Molto comodo, no? Possiamo anche stampare tutti i valori di correlazione per la variabile median_income, magari ordinati in ordine decrescente, con l’istruzione:

il cui output sarebbe:
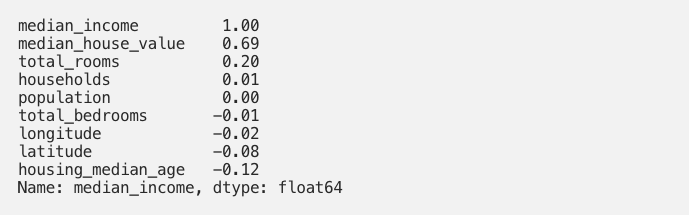
Ma noi vogliamo avere una visione d’insieme della matrice di correlazione del nostro dataset. Per fare ciò potremmo stampare direttamente la matrice rounded_corr_matrix oppure usare la libreria seaborn per visualizzare una heatmap:

Una heatmap, in generale, è una tecnica di data visualization in cui in una struttura bidimensionale (come una tabella) vengono mostrati dei valori associati ad una scala di colori. Nel nostro caso, a colori più scuri corrispondono valori più bassi (con il colore nero che indica il valore -1) mentre a colori più chiari vengono associati valori più alti (con il colore bianco che indica il valore 1). Il metodo di seaborn heatmap prende come primo argomento la struttura dati bidimensionale su cui vogliamo visualizzare la heatmap, e ovviamente nel nostro caso è rappresentata dalla matrice di correlazione. Passiamo al metodo heatmapanche un altro argomento, annot, che settiamo a True; grazie ad esso all’interno delle celle della heatmap potremo visualizzare anche i valori numerici della grandezza che stiamo visualizzando, nel nostro caso le singole correlazioni fra le feature del dataset. L’output è il seguente:
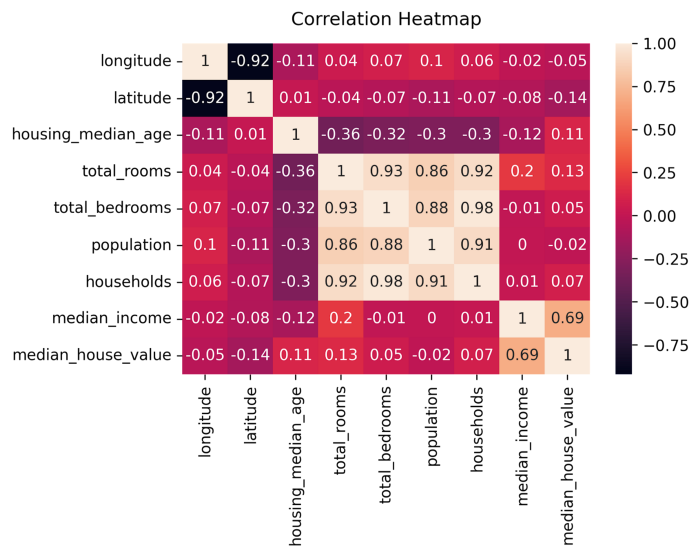
La matrice di correlazione del dataset California housing visualizzata come heatmap.
La comodità della heatmap, come vediamo, risiede nell’immediatezza dell’interpretazione dei dati visualizzati. Ad esempio, è evidente già ad un primo colpo d’occhio che c’è un’alta correlazione fra le feature total_bedrooms e total_rooms (correlazione 0.93, quindi molto vicina a 1), total_rooms e population(0.86), total_bedrooms e households (0.98), e così via. Di contro, avremo una bassa correlazione per le feature latitudee longitude, mentre per valori che sono intorno allo 0 non possiamo identificare alcun tipo di correlazione (es. total_bedrooms e population).
Grazie a pandas possiamo anche prendere un subset delle feature del nostro dataset e stampare la relative matrice di correlazione. Per prendere solo un subset delle feature della nostra matrice di correlazione ci basta creare una lista contenente i nomi delle feature e usarla con la brackets notation (cioè con le parentesi quadre) sulla matrice originaria:

Notiamo che se accediamo semplicemente a features avremo una matrice di dimensioni 9×4 in cui avremo le correlazioni delle 4 feature selezionate con tuttele altre feature del dataset. Usiamo successivamente loc per accedere ad un subset di colonne della struttura 9×4; queste colonne sono esattamente le colonne già specificate, quindi otteniamo una struttura 4×4 per poi usare la solita heatmap. Il risultato è il seguente:
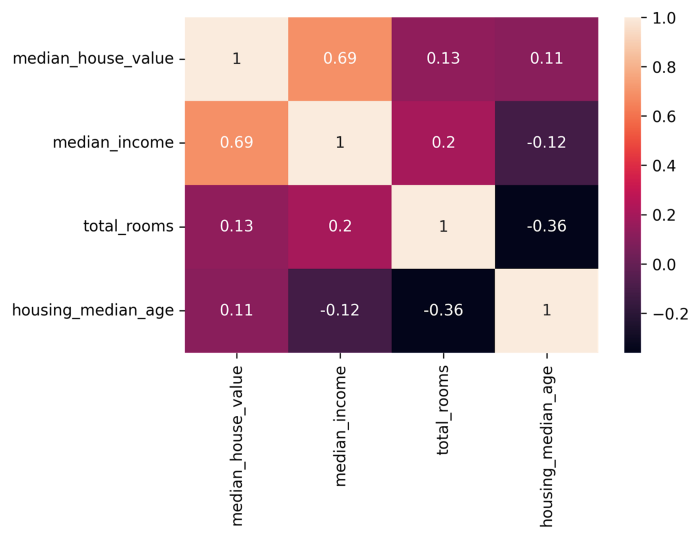
Matrice di correlazione di un subset di features
Come ultimo punto, utilizziamo la funzione di pandas scatter_matrix, che ci fornisce una visualizzazione dei dati ancora più intuitiva rispetto alla matrice di correlazione. Come dice il nome, questa matrice non è composta da numeri, ma da grafici scatter (cioè grafici bidimensionali in cui ogni asse rappresenta una feature). Essa risulta molto utile per visualizzare eventuali relazioni lineari fra le coppie di variabili (un po’come fa la matrice di correlazione, ma da un punto di vista visuale):

L’output visualizzato è il seguente:
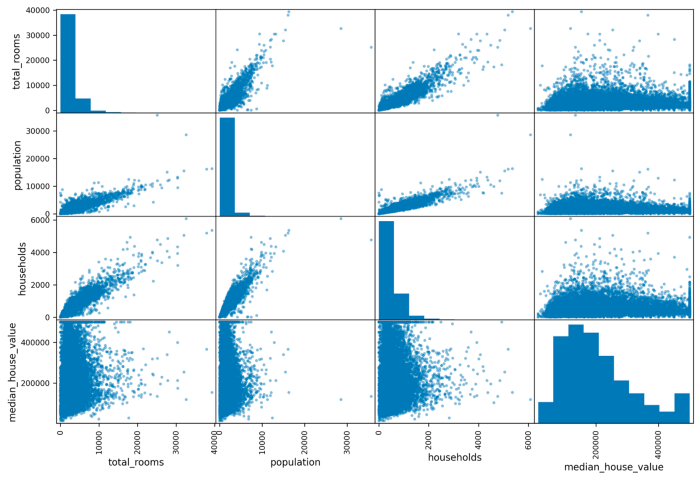
Matrice di correlazione di un subset di features
Notiamo che in questa visualizzazione nella diagonale principale abbiamo degli istogrammi; ricordiamo che sulla diagonale principale ci sarebbero, in teoria, le correlazioni delle variabili con se stesse; se le disegnassimo come grafici scatter avremmo semplicemente delle rette di equazione y = x (cioè sull’asse x e sull’asse y avremmo gli stessi valori: quelli della variabile in esame). Piuttosto che farci vedere una retta, la funzione scatter_matrix ci mostra sulla diagonale principale gli istogrammi delle variabili, il che ci dà un’idea della distribuzione delle singole variabili casuali del dataset. Di contro, è evidente che per determinate coppie di variabili (es. population/total_rooms oppure households/population) ci sia una evidente correlazione positiva e vicina ad 1. Di contro, quasi tutte le variabili presentano una correlazione vicino allo zero con la variabile median_house_value (che per inciso sarebbe quella per noi più interessante in un eventuale modello predittivo di machine learning).
Usi della matrice di correlazione
Ora che abbiamo visto come è costruita una matrice di correlazione e come si può visualizzarne una sotto varie forme con Python, possiamo chiederci quali siano gli usi di questa struttura dati. Nel contesto della programmazione Python, le matrici di correlazione trovano applicazione soprattutto in machine learning, dove vengono utilizzate per fare analisi preliminari al fine di individuare quali modelli predittivi potrebbero essere utilizzati con successo o, alternativamente, quali modelli predittivi potrebbero essere scartati. Ad esempio, se il nostro modello predittivo dovesse rispondere ad un task di regressione (cioè di previsione di un valore continuo) sui prezzi delle case (detta semplice: se dovessimo costruire un agente di machine learning capace di prevedere il prezzo delle abitazioni) potremmo usare una matrice di correlazione sui coefficienti che più ci interessano. In un caso del genere la variabile casuale più interessante sarebbe sicuramente `median_house_value`, e dunque avrebbe senso disegnare una heatmap o una scatter matrix fra questa variabile e le variabili a più alta correlazione:

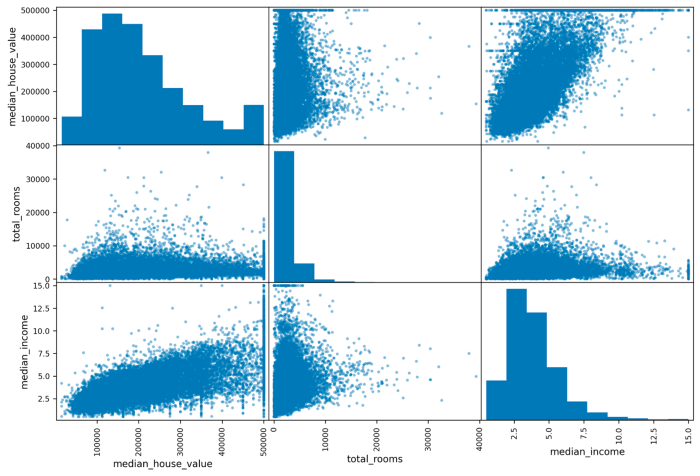
Scatter matrix di un altro subset del dataset California Housing, lievemente più interessante per il Machine Learning.
In questo caso troviamo una correlazione piuttosto evidente fra median_income e median_house_value, il che significa che potremmo provare a costruire e ottimizzare un semplice modello di regressione lineare e addestrarlo. Certo, non otterremmo un modello molto preciso (cosa avremmo potuto aspettarci da una correlazione di 0.69, del resto?), ma è pur sempre un punto di partenza, no?
Bonus track: California, here we come!
Guardando la matrice di correlazione, possiamo notare che un dato abbastanza curioso è dato dal bassissimo valore di correlazione(vicino a -1) fra latitudine e longitudine . Che accadrebbe se provassimo a disegnare uno scatter plot di queste due feature?
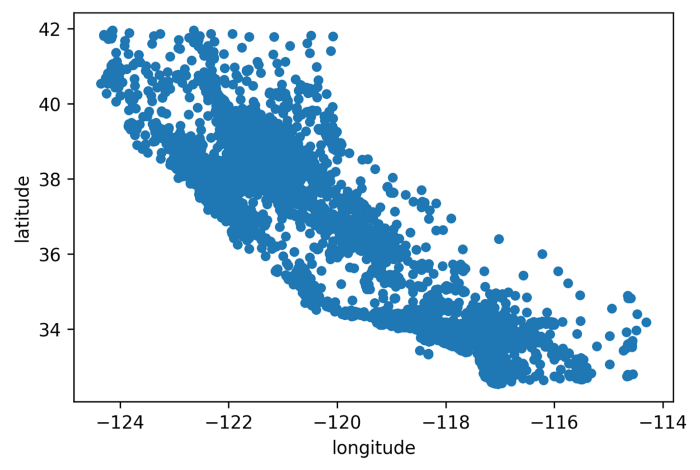
Qualcuno ha detto “California”?
Hey, non sembra proprio la vera California? Ma certo che sì! Il basso valore di correlazione fra latitudine e longitudine è dovuto alla forma geografica della California, che ricorda una retta con coefficente angolare negativo.
Ecco il codice per disegnare questo grafico:

Buono studio e buon coding!













