Correlazione vs. covarianza: è tutto più semplice di quel che sembra

Nello scorso articolo ho parlato di alcuni indici statistici di base che tuttavia possono mettere in soggezione coloro che si affacciano per la prima volta al mondo della data science (varianza, deviazione standard, covarianza).
In questo articolo andiamo a studiare un altro indice sul quale molto spesso si fa confusione, e che tuttavia è molto più semplice da capire e da interpretare di quanto sembri. Stiamo parlando del coefficiente di correlazione.
È un indice che presenta delle analogie e delle differenze con la già vista covarianza, e serve ad uno scopo ben preciso: fornire informazioni sulla presenza (e in caso affermativo dell’andamento) di una relazione fra due variabili casuali. La cosa insolita è che sotto il termine “correlazione” si possono nascondere formule e indici anche molto diversi fra loro a seconda della natura delle variabili sulle quali la correlazione si vuole calcolare.

Paroloni? Sì, forse. La realtà è molto più semplice di quanto possa sembrare. Partiamo da due variabili casuali, i classici “peso” ed “altezza” di un gruppo di (supponiamo) 6 persone:

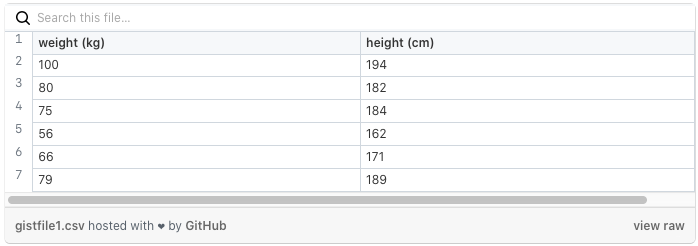
Proviamo inoltre a mettere a grafico queste variabili.

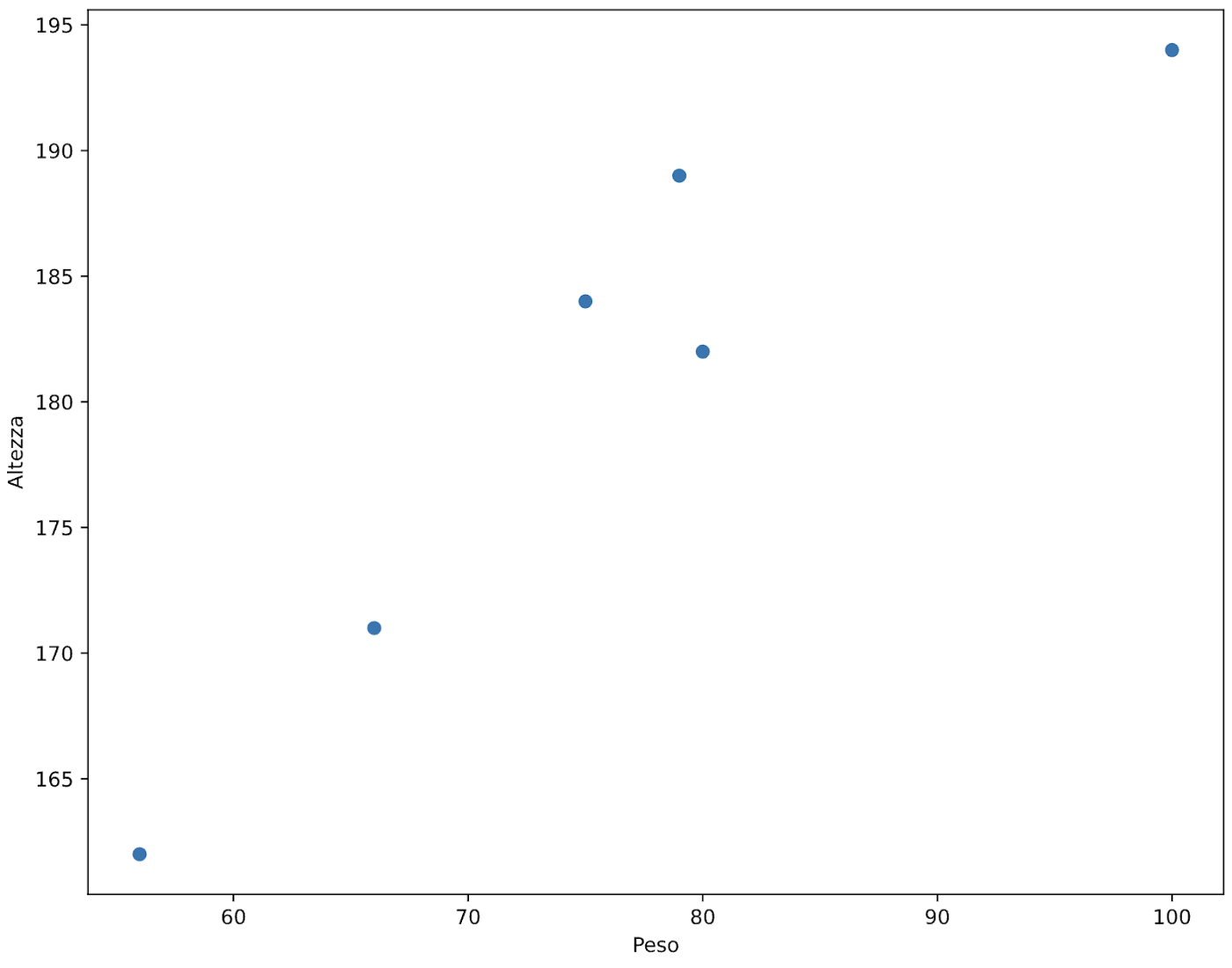
Rappresentazione dei punti del nostro dataset ottenuta con pyplot

Innanzitutto partiamo da una considerazione. Queste variabili non sono scelte a caso, nel senso che rappresentano delle variabili quantitative continue, ovvero variabili che possono assumere dei valori qualsiasi in un insieme numerico o in un suo sottoinsieme. Non sono delle variabili categoriche (variabili i cui valori possibili sono quelli di un predefinito insieme di valori, ad esempio “Colore capelli”, che può avere solo valori predefiniti come “biondo”, “castano”, “nero”, etc). Per le variabili continue come quelle utilizzate nell’esempio, il coefficiente di correlazione che si utilizza è di solito il coefficiente di Pearson, la cui formula è:

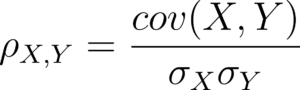
Come vediamo, la correlazione calcolata con il coefficiente di Pearson non è altro che una frazione in cui al numeratore c’è la covarianza fra le variabili X, Y considerate mentre al denominatore c’è il prodotto fra le deviazioni standard delle due variabili (psst, se non hai idea di cosa siano covarianza e deviazione standard di variabili casuali non aver paura! Ci ho già pensato!). Il coefficiente di Pearson serve a individuare se esiste una relazione lineare fra le due variabili casuali. Se si vuole misurare la relazione non lineare si devono usare altri indici (come il coefficiente di Spearman). La formula per calcolare la correlazione su un sample della popolazione è lievemente più complessa, ma la sostanza non cambia: si tratta sempre di una misura della covarianza “normalizzata” rispetto alla deviazione standard delle due variabili. Per calcolare la correlazione dobbiamo quindi:

Calcolare la media delle due variabili X, Y
Calcolare la deviazione standard per ciascuna variabile:
– calcoliamo la differenza per fra ogni campione e la media della variabile e la eleviamo al quadrato
– sommiamo tutti i fattori così ottenuti
– dividiamo per il numero di campioni
– mettiamo sotto radice
Calcolare la covarianza fra X e Y:
– per ogni entry del nostro dataset di riferimento calcoliamo la differenza del valore appartenente a X e la sua media e la moltiplichiamo con la differenza del valore corrispondente appartenente a Y e la sua media
– sommiamo tutti i termini così ottenuti
– dividiamo per il numero di campioni
Più facile a farsi che a dirsi, dunque procediamo. Calcolo della media per “Peso” e “Altezza”:

μ_w = 76KG
μ_h = 180.33cm

Calcoliamo anche la deviazione standard per il peso:

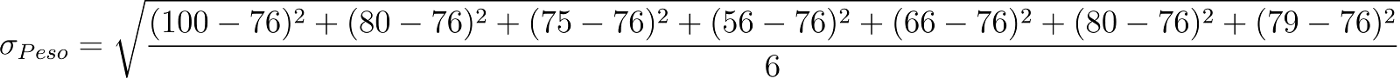
Che ci dà come risultato:

σ_w = 13.5523

Calcoliamo analogamente la dev. standard dell’altezza fino ad ottenere:

σ_w = 10.8115

Per la covarianza dobbiamo prendere invece ciascun punto ( cioè le singole righe della colonna di prima: [100, 194], [80, 182], [75, 184], …), calcolare prima la differenza della componente peso con la sua media, poi la differenza della componente altezza con la sua media e infine moltiplicarle fra loro. Alla fine dividiamo per 6:

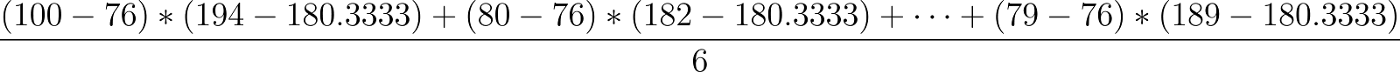
Quello che otteniamo sarà la covarianza fra Peso e altezza:

cov(weight, height) = 163 kg-cm

È finalmente arrivato il momento di calcolare la correlazione di Pearson fra Peso e Altezza:

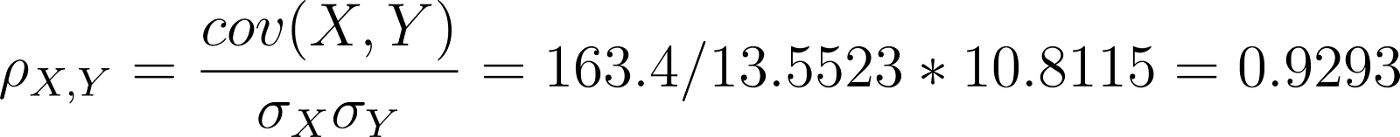
Tutti questi numeri e calcoli ti spaventano?

Per inciso, usando Python e NumPy potremmo giungere al medesimo risultato con tre semplici istruzioni:

Notiamo due cose fondamentali. Innanzitutto la correlazione non ha unità di misura (infatti la coppia kg-cm del numeratore si semplifica con le unità di misura kg e cm delle due deviazioni standard). Già solo questa caratteristica rende la correlazione un indice molto flessibile da utilizzare. L’altra considerazione interessantissima sulla correlazione è che essa ha un intervallo ben definito. Essa è infatti sempre compresa fra -1 e 1. In particolare, in maniera simile alla covarianza:

se la correlazione è compresa fra -1 e 0 vuol dire che le due variabili sono inversamente correlate: vale a dire che all’aumentare di una l’altra decresce
se la correlazione è uguale a 0 non esiste alcuna correlazione lineare fra le variabili
se la correlazione è compresa fra 0 e 1 vuol dire che le due variabili sono direttamente correlate: all’aumentare di una aumenta anche l’altra
Non solo: più la correlazione è vicina a -1, più sarà “evidente” e alto il grado di correlazione “inversa” fra le due variabili. Più la correlazione è vicina a 1, più sarà alto il grado di correlazione “diretta” fra le due variabili. Infine più la correlazione è vicina allo 0 più le due variabili saranno poco correlate fra loro. Nel nostro caso il valore 0.929 è molto vicino ad 1, il che indica un alto grado di correlazione.

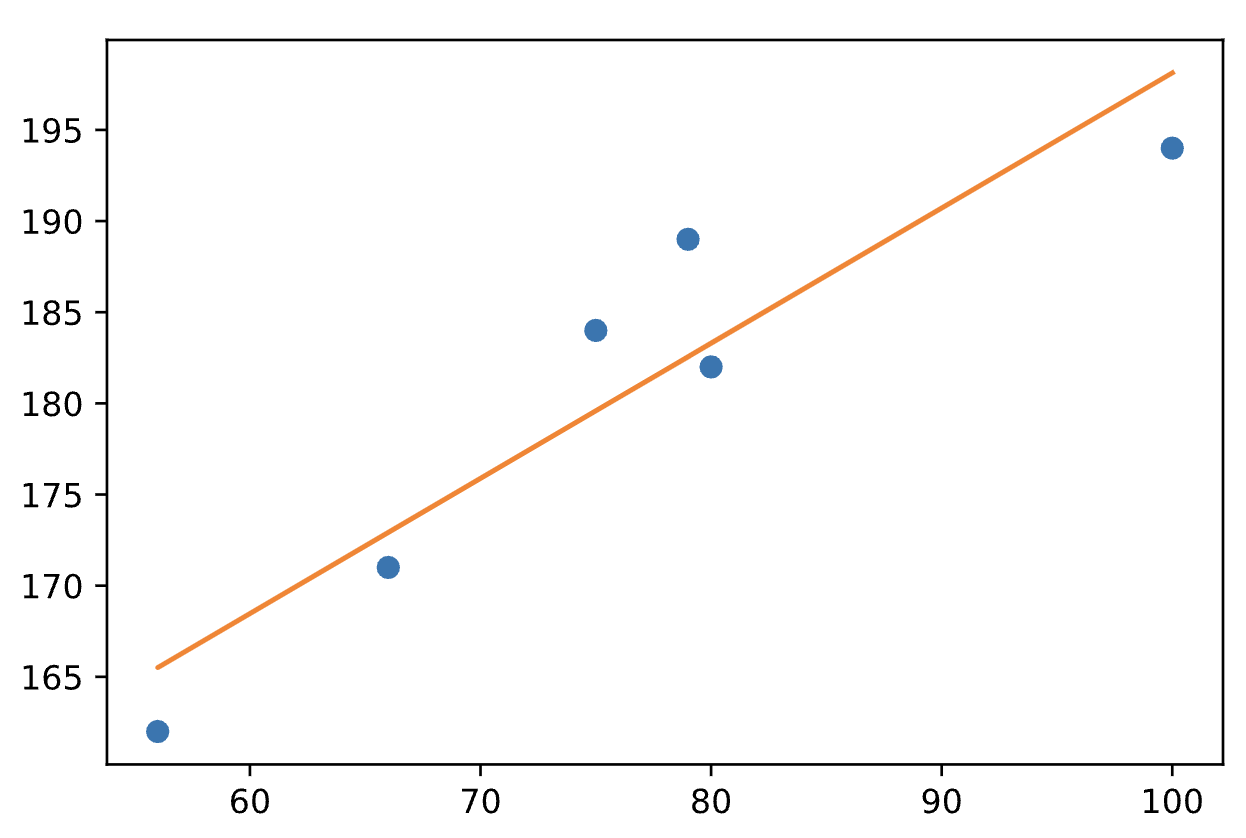
Del resto in questo caso era abbastanza evidente anche ad occhio nudo che ci fosse un alto grado di correlazione fra le variabili, come si può notare da questo grafico:

Disegnamo adesso gli altri 2 casi di correlazione fra 2 variabili. Di seguito correlazione vicina a -1:

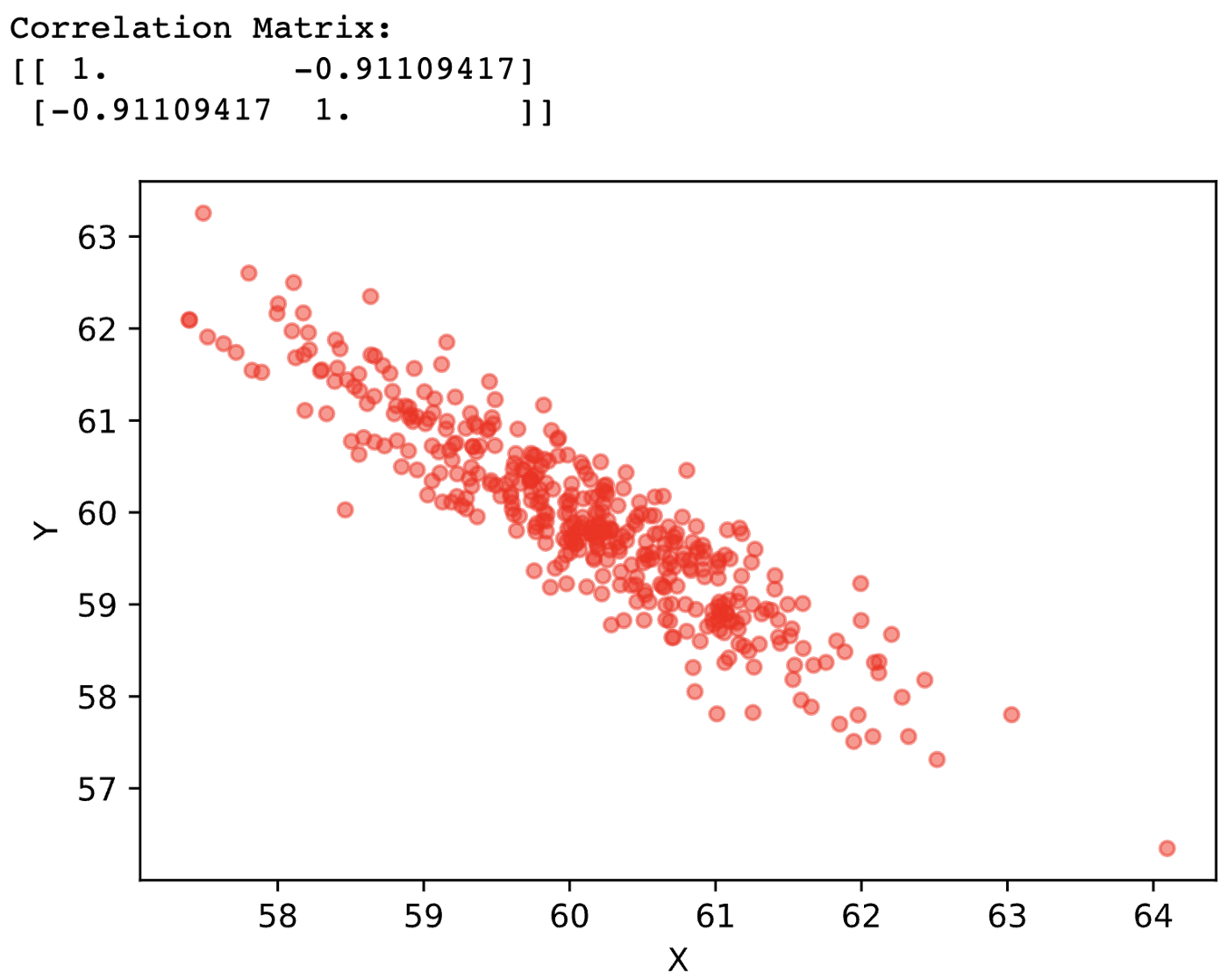
Di seguito correlazione vicina a 0:

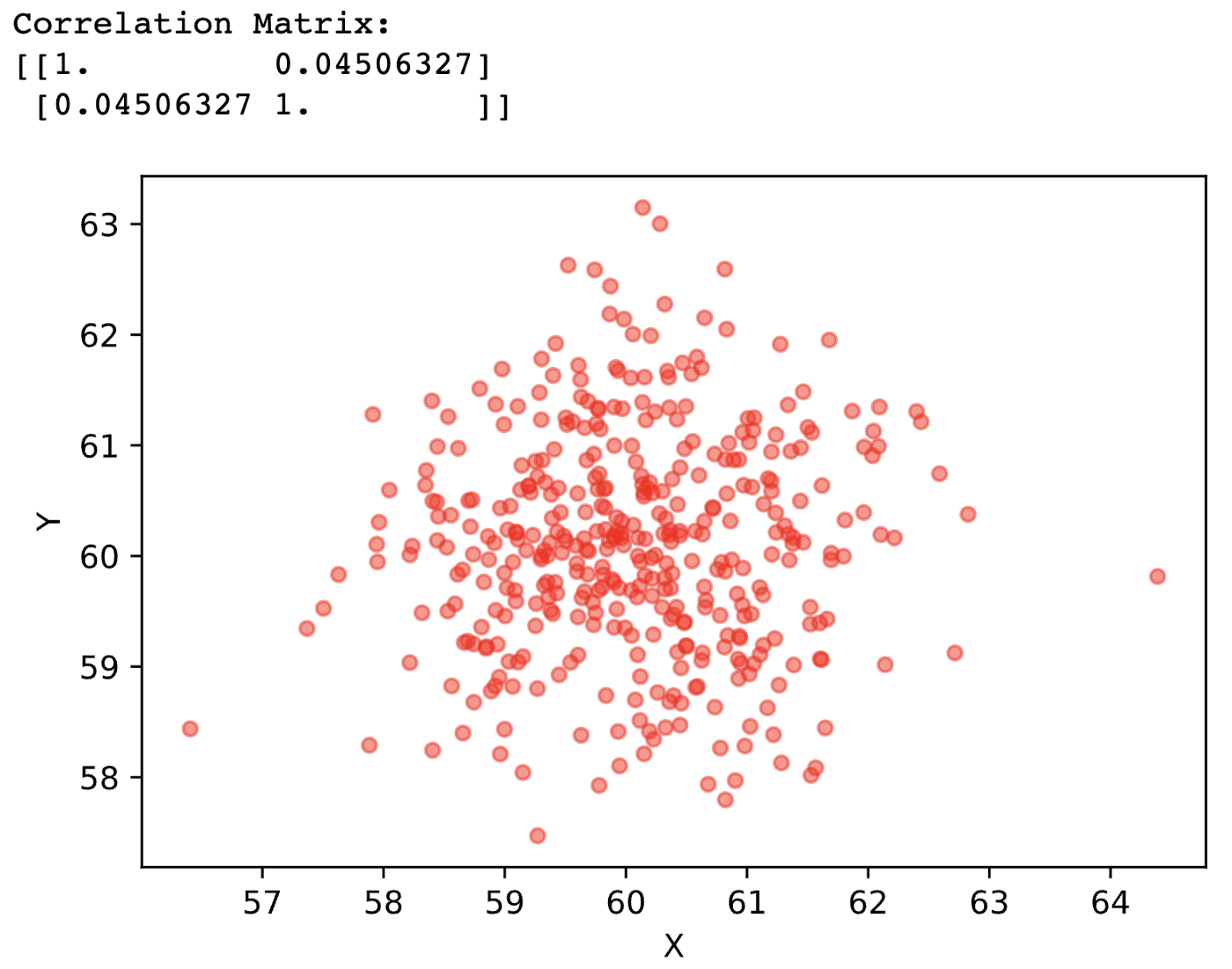
Prima di ogni grafico ho stampato con Python la matrice di correlazione. Essa è simile alla matrice di covarianza, e cioè è una matrice triangolare quadrata in cui troviamo sulla diagonale principale la correlazione di ogni variabile con se stessa(ergo massima correlazione, cioè 1), mentre nelle altre posizioni abbiamo la correlazione delle variabili corrispondenti alla riga e delle variabili corrispondenti alla colonna. Ma parlerò della matrice di covarianza in un altro articolo.

Prima di concludere, vediamo quali sono le analogie e le differenze fra la covarianza e la correlazione.